오류 검출, 정정
오류 검출 및 정정 기술
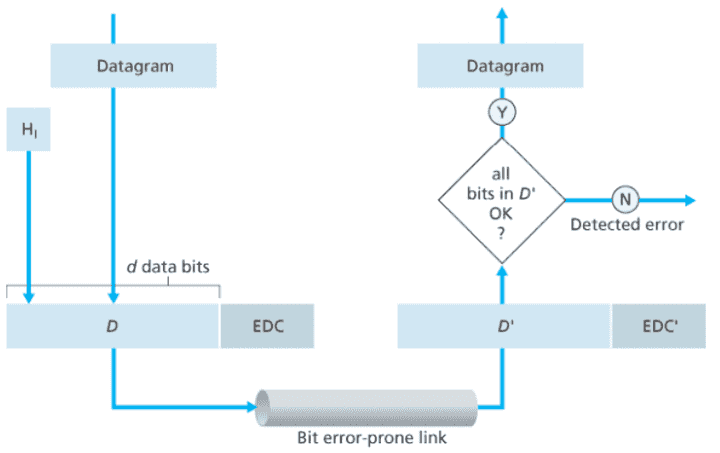
비트 오류를 방지하기 위해 송신 노드에서 데이터 D에 오류 검출 및 정정 비트들(EDC)를 첨가한다.
송신되는 데이터 D와 EDC는 전송 도중 변경될 수 있다.
즉, 수신자는 변경의 가능성이 있는 비트로 오류 검출 여부를 확인하여야 한다.
오류 검출 및 정정 기술을 사용하더라도 여전히 미검출된 비트 오류(undetected bit error)가 있을 수 있다.
즉, 수신자는 잘못된 데이터그램을 네트워크 계층으로 전달할 수 있고, 프레임 헤더의 다른 필드의 내용이 잘못된 것을 모를 수도 있다.
따라서 오류를 감지하지 못할 확률이 낮은 기법을 선택해야한다. (대체로 확률이 낮을 수록 오버헤드가 크다.)
패리티 검사
단일 패리티 비트
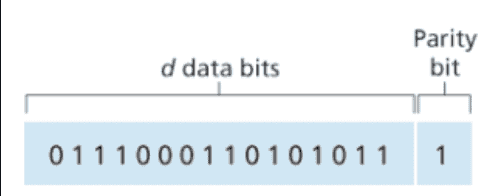
데이터 D가 d개의 비트를 갖고 있다고 가정하자.
짝수 패리티 기법에서는 단순히 D에 한개의 Parity bit를 추가하고, d+1개의 비트에서 1의 총개수가 짝수가 되도록 Parity bit 을 선택한다.
수신자는 수신된 d+1개의 bit에서 1의 개수가 짝수임을 확인한다.
(당연히 홀수라면 1의 개수를 홀수로 정한다.)
이 방법의 경우 홀수개의 비트 오류는 검출할 수 있지만 짝수개의 비트 오류는 검출할 수 없다.
측정에 의하면 오류는 종종 버스트(burst)의 형태로 몰려서 발생하기 때문에 위 방법은 50% 확률로 오류를 검출할 수 있다.
2차원 패리티

데이터 D에 있는 d 비트들은 i개의 행과 j개의 열로 나뉜다.
나뉜 각각의 행과 열에 대해 하나의 패리티 값이 계산된다.
2차원 패리티 기법에서는 반전된 비트를 포함하는 열과 행에 대한 패리티에 오류가 생긴다.
따라서 수신자는 단일 비트의 오류 발생을 검출할 수 뿐만 아니라 열과 행의 인덱스 값을 통해 오류를 정정할 수도 있다.
또, 단일 패리티와는 달리 임의의 2개의 오류도 검출할 수 있다. (그러나 정정할 수 없다.)
순방향 오류 정정(forward error correction, FEC)
오류를 검출 및 정정하는 수신자의 능력을 FEC라고한다.
FEC 기술은 송신자에게 요구하는 재전송 횟수를 줄일 수 있다.
이를 통해 NAK 패킷을 수신하고 재전송된 패킷이 수신자로 되돌아가는 소요 시간이 왕복 지연 시간을 기다릴 필요가 없어진다.
체크섬 방법
d 비트들을 k 비트 정수처럼 다루어 이 k비트 정수들을 더해서 그 결괏값을 오류 검출 비트들로 사용한다.
체크섬 동작 과정
인터넷 체크섬(Internet checksum)
- 더한 값의 1의 보수가 인터넷 체크섬이 되며, 이것을 세그먼트 헤더에 넣어준다.
- 수신자는 수신 데이터 합의 1의 보수를 취한 후 그 결과가 모두 1인 비트로 구성되어 있는지 계산함으로써 체크섬을 검사한다.
- 그 결과가 모두 1인 비트로 구성되어 있는지 계산함으로써 체크섬을 검사한다.
체크섬 방법은 상대적으로 패킷 오버헤드가 적어 TCP와 UDP에서 사용된다. 그러나 순환 중복 검사(CRC)와 비교하면 오류면에서 취약하다.
TCP와 UDP에서 사용하는 이유는 TCP와 UDP는 소프트웨어로 구현되어 간단하고 빠른 오류 검출 기법이 필요한 반면 링크 계층은 네트워크 어댑터 안에 하드웨어로 구현되어 순환 중복 검사(CRC) 를 사용한다.
순환 중복 검사(CRC)
오늘날 컴퓨터 네트워크에서 널리 사용되는 오류 검출 기술은 순환 중복 검사(cyclic redundancy check, CRC) 코드 를 사용한다.
CRC 코드는 전송되는 비트열에 있는 0과 1 값을 계수로 갖는 다항식처럼 비트열을 생각할 수 있고, 또한 비트열에 적용되는 연산을 다항식 연산으로 이해하는 것이 가능하기 때문에 다항식 코드(polynomial code)로도 알려졌다.
CRC 동작 과정
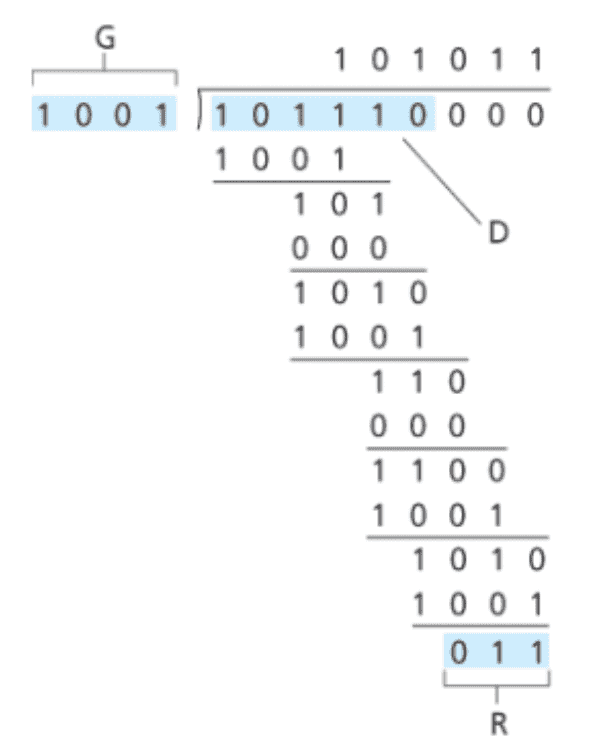
- 먼저 송신자와 수신자는 G로 표기되는 생성자로 알려진 r+1 비트 패턴에 대해 합의한다. 이때 G의 최상위 비트는 1이어야 한다.
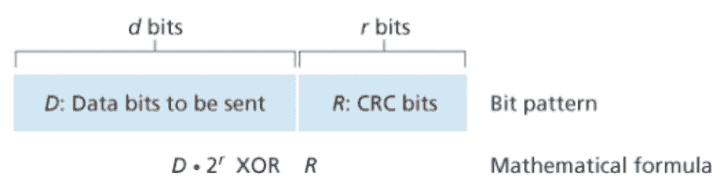
- 송신자는 D에 r개의 추가 비트 R을 선택해서 D 뒤에 덧붙인다.
- 일반 이진 연산에서 2^k을 곱하는 것은 비트 패턴을 k개의 위치만큼 왼쪽으로 이동하는 것과 같다. 즉, 위 그림의 식을 통해 d+r 패턴을 만들 수 있다.
- 만들어진 d+r 비트 패턴은 모듈로 2 연산을 이용하면 G로 정확히 나누어진다.
- 수신자는 d+r개의 수신 비트를 G로 나눈다. 만일 나머지가 0이 아니면 오류가 발생한 것이다.
모든 CRC 검사는 덧셈의 올림이나 뺄셈의 빌림이 없는 모듈로 2 연산을 사용한다.
즉, 이는 피연산자를 비트별로 XOR한 것과 같다.
e.g.
1011 XOR 0101 = 1110
1001 XOR 1101 = 0100
1011 - 0101 = 1110
1001 - 1101 = 0100R을 계산하는 과정
먼저 다음과 같은 식을 만족하는 n이 있도록 하는 R을 구해야한다.
D x 2^r XOR R = nG즉, D x 2^r XOR R을 나머지 없이 G로 나눌 수 있도록 R을 선택해야 한다. 이 식의 양쪽에 R을 XOR(즉, 올림 없는 모듈로 2 덧셈)하면 다음과 같다.
D x 2^r = nG XOR R이 식은 D x 2^r 을 G로 나누면 나머지가 정확히 R이 되는 것을 뜻한다.
다시 말해, 다음 처럼 R을 계산할 수 있다.
R = 나머지 D x 2^r / Ge.g.