분할-정복1
이진탐색
-
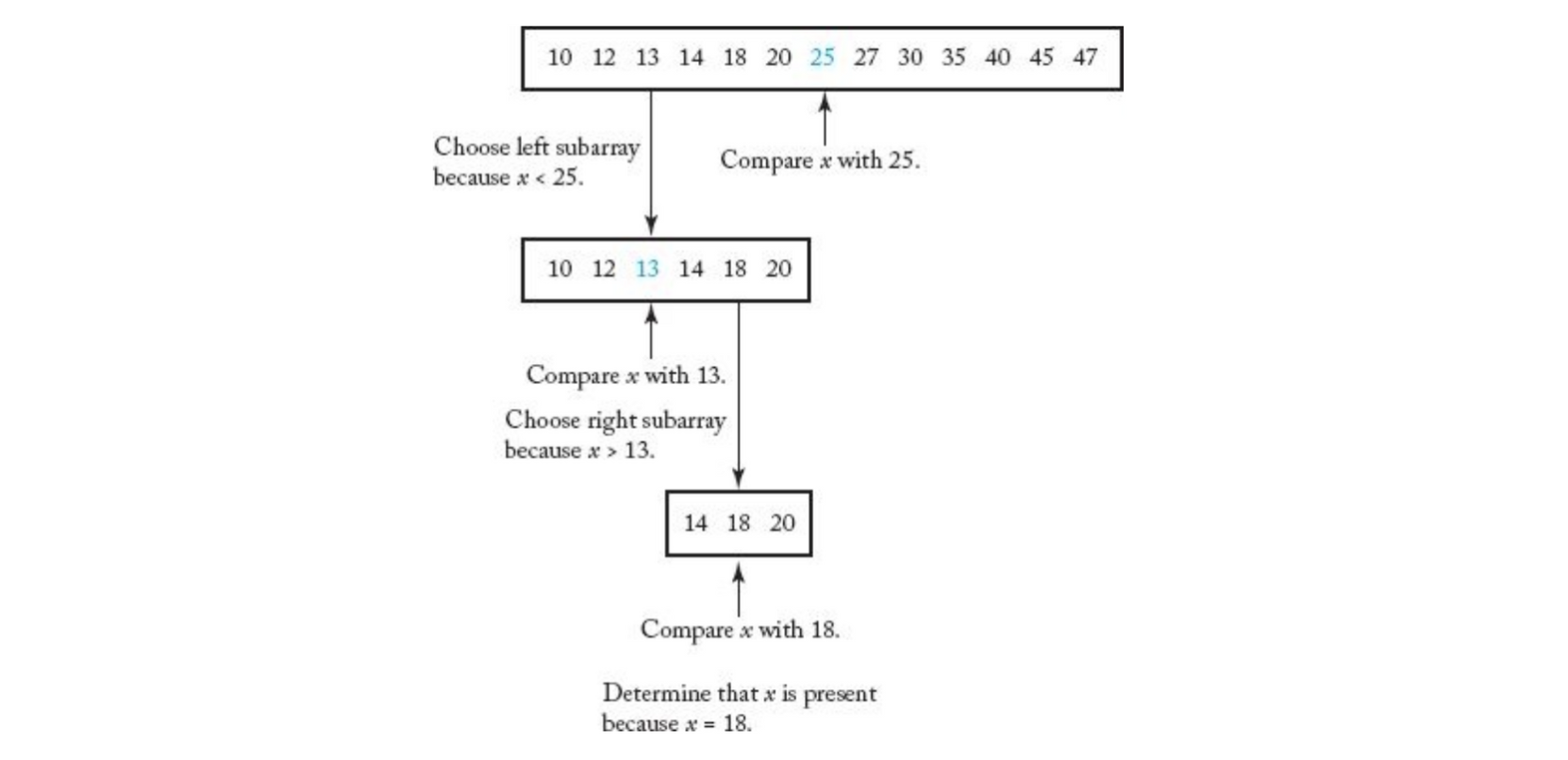
반드시 이미 정렬된 배열에 대해 사용
-
배열에서 임의의 값을 선택, 찾으려는 값보다 임의의 값이 크면 임의의 값 왼쪽에서 재탐색(재귀).
-
찾으려는 값보다 임의의 값이 작으면, 임의의 값 오른쪽에서 재탐색(재귀)
public class BS_recur { public static int binarySearch(int[] arr, int start, int end, int value) { // 정렬되어 있는 배열 arr의 start부터 end까지에서 value의 idx를 찾는 함수 if (start > end) //start가 end보다 큰 경우 탐색 실패, 찾으려는 값이 없음 return -1; else if (start == end) { // start가 end와 같은 경우 if (arr[start] == value) //찾으려는 값이 start인덱스에 있는 경우 return start; //(찾음!) else //찾으려는 값이 없음 return -1; } else { int mid = (start + end) / 2; //중간값 if (arr[mid] == value) //중간 값이 찾으려는 값인 경우 return mid; //(찾음!) else if (arr[mid] > value) //찾으려는 값보다 중간값이 큰 경우 return binarySearch(arr, start, mid - 1, value); //왼쪽에서 재탐색(재귀) else //찾으려는 값보다 중간값이 작은 경우 return binarySearch(arr, mid + 1, end, value); //오른쪽에서 재탐색(재귀) } } } -
시간복잡도 분석
- 처음에 입력된 개수 n이라 하면 첫 시행 후 n/2, 재시행 후 n/2 x 1/2 …
- k번의 시행 후에 (1/2)^k x n 이고, 최악의 경우, 마지막에 1개가 남을때이므로 (1/2)^k x n ~= 1
- 양변에 2^k를 곱해주면, n ~= 2^k이다. 여기서, 양변에 2를 밑으로 하는 로그를 취하면
- k = log_2(n), 시간복잡도는 O(logn)으로 나타낼 수 있다. (상수 무시)
합병 정렬(Merge sort)
public class MergeSort {
public static void merge_sort(int array[],int start, int end){
if(end-start >= 1){
int mid = (start+end)/2;
merge_sort(array, start, mid);
merge_sort(array, mid+1, end);
int l = start;
int r = mid+1;
int newArray[] = new int[end-start+1];
int idx = 0;
while(l <= mid && r <= end){
if(array[l] < array[r]){
newArray[idx++] = array[l++];
}
else{
newArray[idx++] = array[r++];
}
}
while(l <= mid){
newArray[idx++] = array[l++];
}
while(r <= end){
newArray[idx++] = array[r++];
}
idx = 0;
for(int i = start ; i <= end ; i++){
array[i] = newArray[idx++];
}
}
}
}
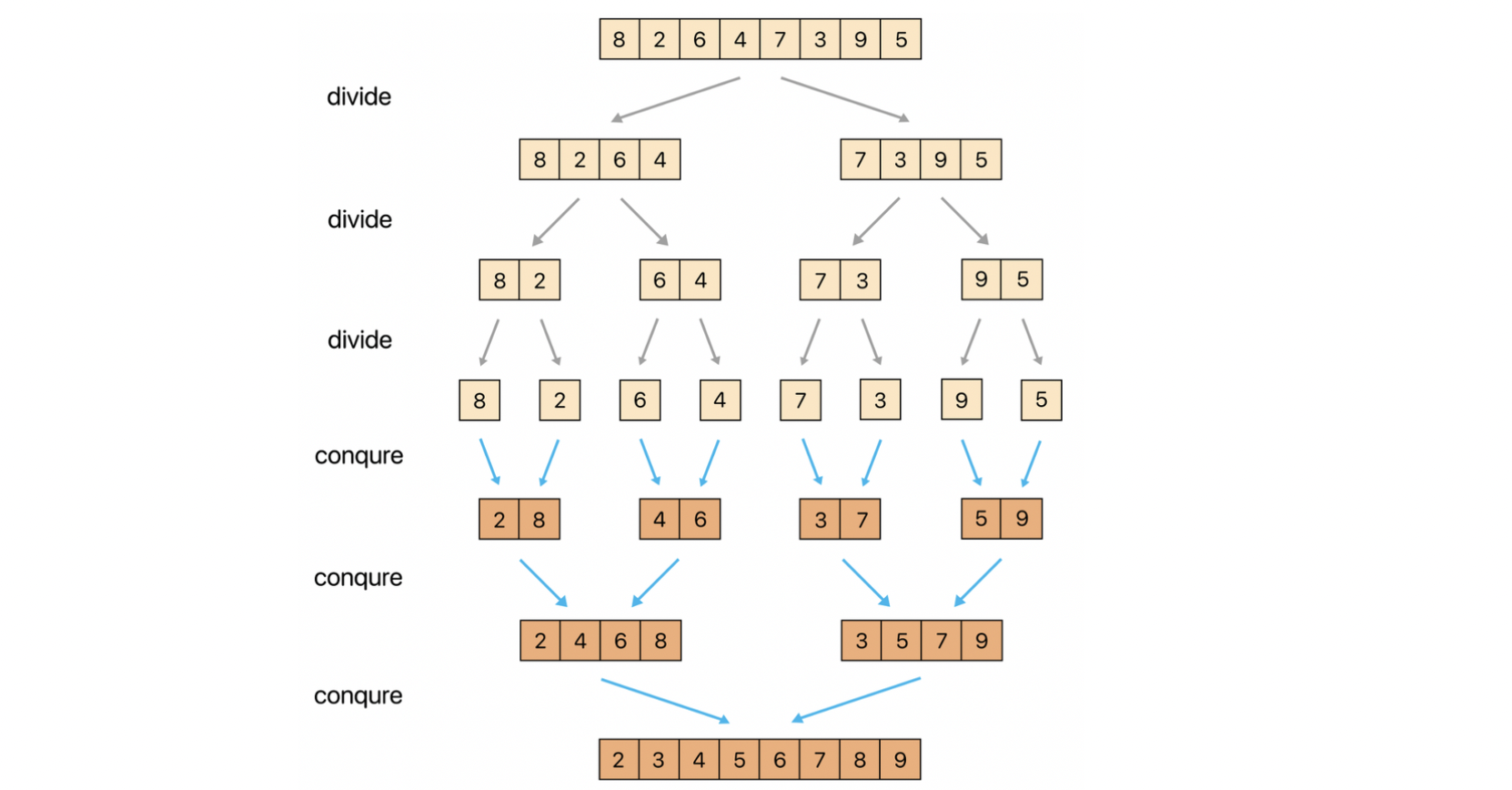
- 시간복잡도
- 배열의 길이 n이라 할때, 단계의 높이는 logn을 따르고, 병합시 비교는 배열의 길이만큼의 횟수가 필요하기 때문에 n이다. 따라서 시간복잡도 O(nlogn)이다.
- 최악의 경우 및 점화식 분석